Quantum contextual sets have been recognized as resources for universal quantum computation, quantum steering and quantum communication. Therefore, in our paper in “Quantum” (Impact Factor 6.4) Mladen Pavičić, “Quantum Contextuality,” Quantum 7, 953 (2023); DOI 10.22331 q-2023-03-17-953 we focus on engineering the sets that support those resources and on determining their structures and properties. Such engineering and subsequent implementation rely on discrimination between statistics of measurement data of quantum states and those of their classical counterparts. Their discriminators are hypergraphs which determines how states supporting a computation or communication are arranged.
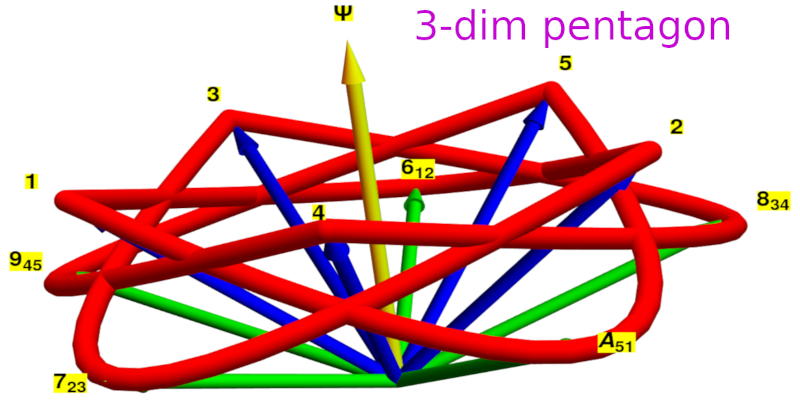
It turns out that contextual quantum non-binary hypergraphs, in contrast to classical binary ones, are essential for designing quantum computation and communication and that their structure and implementation rely on such non-binary vs. binary differentiation. We are able to generate arbitrarily many contextual sets from simplest possible vector components and then make use of their structure by implementing the hypergraphs with the help of YES-NO measurements so as to collect data from each gate/edge and then postselect them. At the same time this procedure shows us that we have to carry out measurements on complete set of states before we postselect them. As an example the Klyachko pentagon cannot lie in a plane, as shown in the figure; only its postselected states do.
Other considered discriminators are six hypergraph inequalities. They follow from two kinds of statistics of data. One kind of statistics, often applied in the literature, turn out to be inappropriate and consequently two kinds of inequalities turn out not to be noncontextuality inequalities. Results are obtained by making use of universal automated algorithms which generate hypergraphs with both odd and even numbers of hyperedges in any odd and even dimensional space – in this paper, from the smallest contextual set with just three hyperedges and three vertices to arbitrarily many contextual sets in up to 8-dimensional spaces. Higher dimensions are computationally demanding although feasible.