Recently obtained results published in Pavičić, M., Arbitrarily exhaustive hypergraph generation of 4-, 6-, 8-, 16-, and 32-dimensional quantum contextual sets, Physical Review A, 95, 06212–1-25 (2017) will be implemented in a series of experiments in the CEMS Research Unit Photonics and Quantum Optics.
Quantum contextuality is a property of quantum systems not to have predetermined values of their observables, in contrast to classical systems. Take an entangled photon pair. Each of the photons is genuinely unpolarized before we let them through polarizers. After polarizers, measurements find the photons in definite polarization states. Can we assume that these polarizations were somehow predetermined when the pair was created? The so-called contextual sets of states of photons prove that we cannot. Such sets are not of just of a foundational theoretical interest. Recently it turned out that the “contextuality is the source of a quantum computer’s power” (Nature; cited in the paper). Therefore, it is important for future applications and implementations to find new classes, instances, and structure of contextual sets as well as to design algorithms and programs for obtaining them. In this paper, arbitrary exhaustive hypergraph-based generation of the most explored contextual sets, Kochen-Specker (KS) ones, is carried out in up to 32 dimensions.
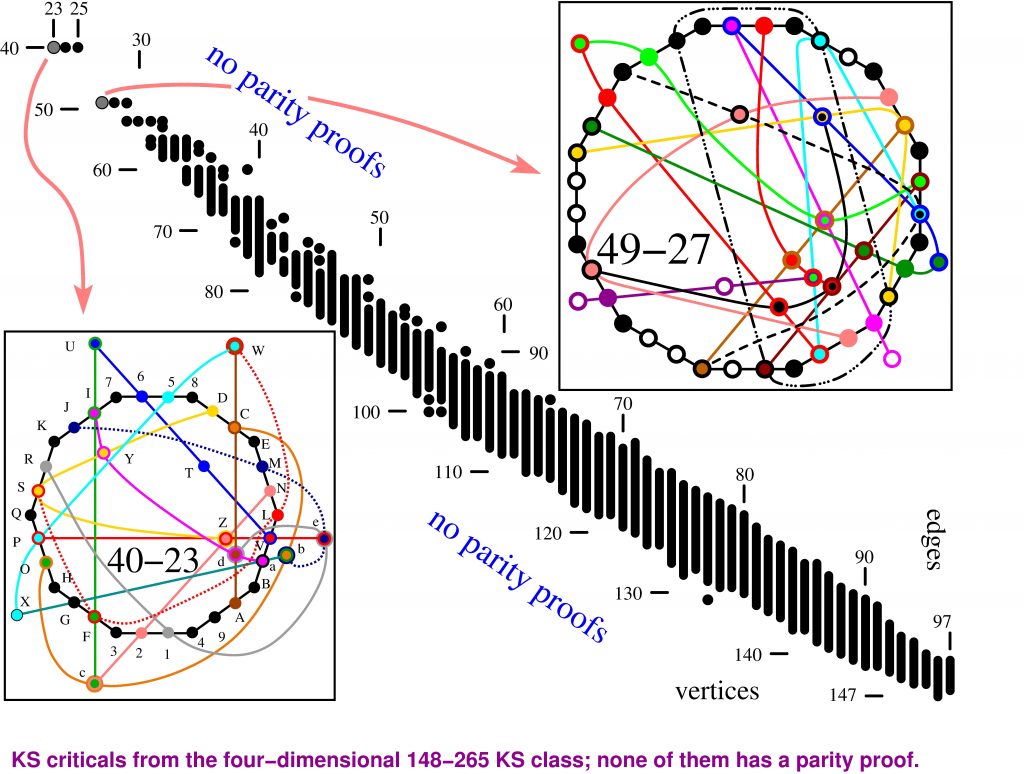
Twelve classes of critical KS sets (the ones that cannot be simplified further) are generated and analyzed, huge number of novel types and instances of them obtained and numerous properties of theirs found. Several thousand times more types and instances of KS sets than previously known are generated. All KS sets in three of the classes and in the upper part of a fourth are novel. The generation was carried out with the help of McKay-Megill-Pavičić (MMP) hypergraph language, algorithms, and programs which generate KS sets (see the feature image for two hypergraphs of 8-dim KS sets; also the figure below) strictly following their definition from the Kochen-Specker theorem, which itself celebrates semicentennial this year. This is in contrast to parity proof based algorithms which prevail in the literature and for which the majority of KS sets and even a whole KS class (as the one shown in the Figure below) are simply invisible.